为什么三角形的面积公式是底乘高除以2?这是我见过最好的解释

求三角形面积的数学公式:
底×高÷2
求三角形面积的数学公式是这样的吧?那么为什么通过这个公式就能求得三角形的面积呢?
“这个问题我倒是没有想过……”
“我上小学的时候,老师就是这么教的……”
这就是错误的数学学习方法的开端。

当然,也有人会回答:
“那是因为三角形的面积是相对应的四边形的面积的一半。”
那么我又要问了,
为什么四边形的面积运算公式就是“底×高”呢?
要想回答出这个“为什么”,那么你就必须对计算面积的数学定义有着深刻的理解和认识。
让我们先来算一下,在下面这个图形当中,包含了多少个基准的小正方形(比如1cm 2 的正方形)。
在下面的图片当中,每一个格子,长和宽都是1cm。
图片上的长方形,长(底边)为8cm,宽(高)为5cm。

在长方形当中,横着数一排是8个正方形的小格子,竖着数一列是5个。那么,在这个长方形里面,总共有多少个正方形小格子?
8×5=40个
因为1个小正方形格子的面积是1cm 2 ,那么长方形的面积就是40cm 2 。
那么,在计算长方形面积的时候,
我们就能够用“底×高”的方法来计算。
那么,平行四边形又怎样计算面积呢?
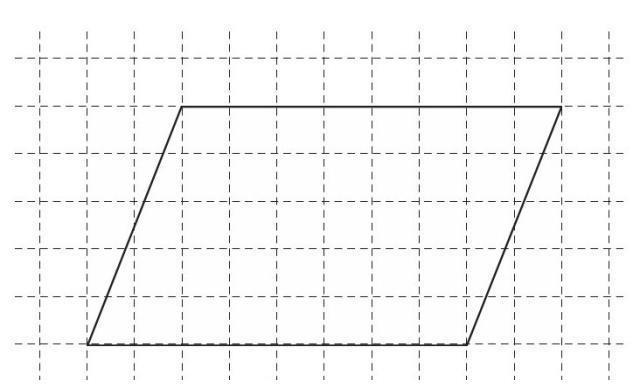
在这个平行四边形当中,有许多正方形小格子是不完整的,那么我们就很难数得出它包含了多少个正方形小格子。那么,我们将它进行如下变形
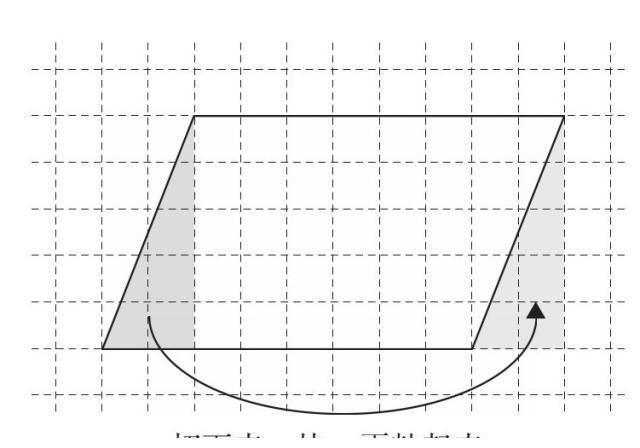
这样一来就和先前的长方形变得一样了:
底×高
那么它所包含的小正方形的个数,很快就能算得出来。
接下来,我们再回过头来说三角形。
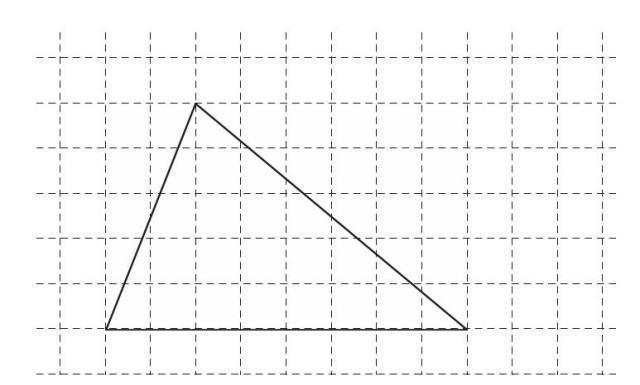
与平行四边形同样的道理,因为有许多正方形小格子是不完整的,所以我们就很难数得出它包含了多少个。如下图所示,我们将这个三角形逆向翻转过来,
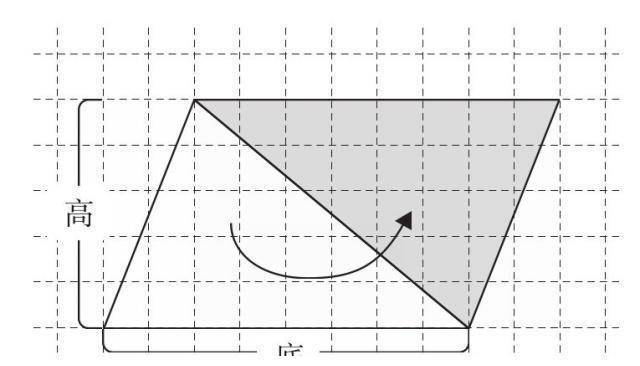
这样一来,就和之前的平行四边形是一样的了。
那么,我们就可以算出平行四边形的面积为:
底×高
然而,图片当中的平行四边形是由最初的两个三角形合起来的,那么我们就可以得出,平行四边形的面积是最初的三角形面积的2倍。那么三角形的面积就应该为:
底×高÷2
怎么样?你有什么感触没有?
这就是三角形面积公式背后的原理。如果你能够理解整个原理,那么,三角形面积公式也好,四边形面积公式也好,就没有死记硬背的必要了。同样,关于梯形的面积公式:
(上底+下底)×高÷2
我们也可以举一反三,从而轻易的找出背后的“原理”。不仅仅如此,像这种思考方式(通过对小面积单元格的叠加计算,从而得出整体的面积),对于即将要学到的“积分”课程,想必同样会在理解上给你带来很大的帮助。
如果不想死记硬背数学定义和公式,那么在一开始,你就必须要找出它背后所蕴藏的“原理”。另外,你不能仅仅
只是理解这么一个数学定义,还要搞明白它与其他的数学定义之间有着怎样的联系,这就需要你对这些原理有着全面性的掌握。
再者,当你掌握了数学公式背后所蕴含的原理的同时,好奇心也得到了极大的满足。你自然会感觉到:
“哦,原来是这么一回事!”
“还真是有意思啊!”
继而让你感觉到其实学习数学也很有趣,这也是“不死记硬背”的学习方法所能带来的趣味性。当你搞懂了某个数学公式背后的原理之后,想一想,如何才能活学活用,而不是刻意的去死记硬背,这就是学习数学的关键诀窍。